Clinton’s Equal Central Angle Conjecture
This document can also be downloaded as a PDF. Click here
BY JOSEPH D. CLINTON, PolyModular, Ltd.
BACKGROUND
In 1937 Michael Goldberg introduced “a class of multi-symmetric polyhedra” consisting of twelve pentagons, eight quadrilaterals or four triangles and all additional faces being hexagons. Thus he introduced the fact “trihedral polyhedra which posses the same number of hexagonal faces in addition to 12 (8, or 4) regularly and symmetrically disposed pentagons (quadrilaterals, or triangles) can be opologically different.” Ref 1
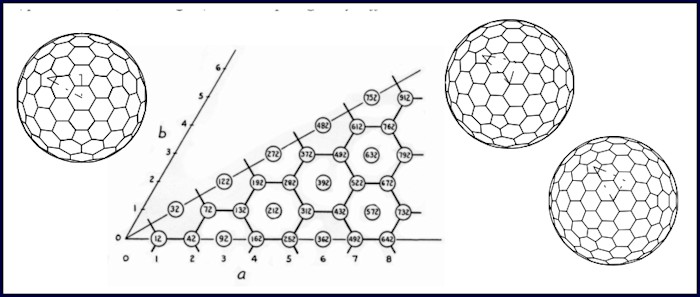
Figure 1. Goldberg’s polyhedra
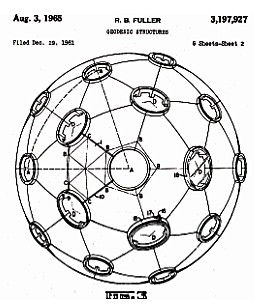
Figure 2. Buckminster Fuller’s geodesic structure
Buckminster Fuller recognized the same patterns of hexagons being clustered around the twelve pentagons of his icosahedron based geodesic forms, as can be seen in his 1965 “Geodesic Structures” patent US 3,197,927. Ref 2 He took advantage of this characteristic to provide circular openings inside the pentagons and hexagons while retaining the triangular structuring between. The cylindrical holes provided additional stiffness and the elements between the holes would nest easily for packing and shipping during disassembly. Fuller applied his concept to structures he referred to as the “Fly’s Eye” structures. Ref 3
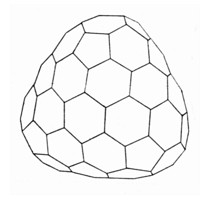
Figure 3. Fowler’s C120
After Harold Kroto and Richard Smalley published their discovery of the Carbon molecule C60 in 1985, Ref 4, P.W. Fowler suggested that “icosahedral carbon clusters with pentagonal and hexagonal faces are Goldberg polyhedra. They have 20(b2 + bc + c2) atoms, where b and c are non-negative integers, and obey an electroncounting rule similar to the famous Hückel (4n + 2) prescription. When b – c is divisible by 3 the cluster has a multiple of 60 atoms and is closed-shell.” He also suggested “a tetrahedral structure…is the best candidate for C120.” Ref 5
Another application of the Goldberg polyhedra came from the work of John P Snyder when he published “an equal-area map projection for polyhedral globes” in 1992. Ref 6
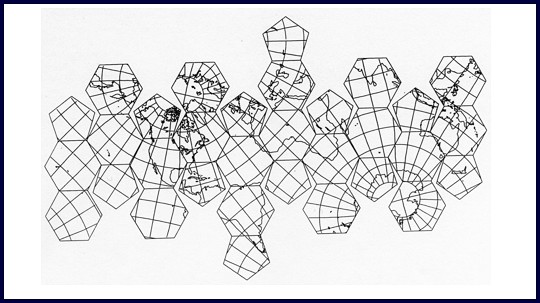
Figure 4. Snyder’s EMAP grid
As a further advancement of the Snyder EMAP grid a class of spatial data structures called Geodesic discrete global grid systems (Geodesic DGGS) has been studied. Ref 7, 8 One such grid, the Icosahedral Snyder Equal Area grid (ISEA), subdivides the face of an icosahedron into hexagons and uses the Snyder equal area projection to transform the hexagon grid to the sphere. The resulting Goldberg polyhedron consists of 12 pentagons with clusters of hexagons covering the remaining area of the sphere. The coarseness of the hexagonal grid determines the number of overlapping Goldberg polyhedra.
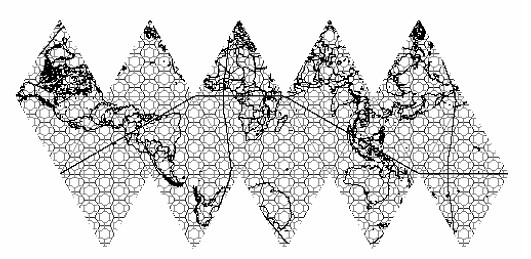
Figure 5. Geodesic DGGS-ISEA Ref 9
In the late 1960’s under a NASA research project thirteen geometrical methods of describing a three-way grid for tessellating the surface of a sphere after Fuller’s methods were studied. Ref 10 Many others have been studied and reported in the literature since.
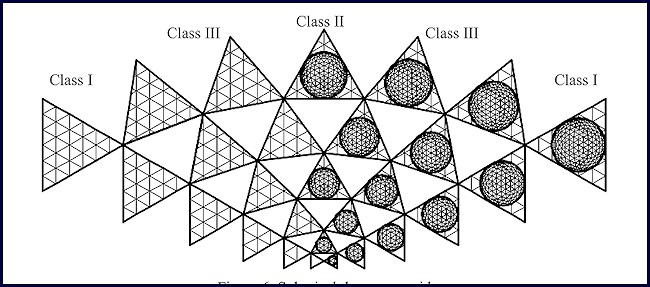
Figure 6. Spherical three way grid
If select vertices are removed from such grids the Goldberg polyhedra emerges. The topologies of these many geometrical solutions remain the same within each group.
Figure 7. Seven geometries of a Goldberg icosahedral polyhedron
GOLDBERG’S POLYHEDRA’S TOPOLOGY
Figure 8. Goldberg’s polyhedra where a = 1 and b = 2
“Topologically, the arrangement of the hexagons in a triangular patch is the same as in a 30º sector of a regular honeycomb arrangement of hexagons…Using a, b as the inclined coordinates (60º between axes) of the vertex of a patch, the square of the distance from the center of the patch to the vertex is equal to a2 + ab + b2…the total number of faces bounding the ‘polyhedron’ is 10(a2 + ab +b2)+2;” for the icosahedral system, 4(a2 + ab +b2)+2 for the octahedral system, and 2(a2 + ab +b2)+2 for the tetrahedral system. Ref 1
It can be shown that for the each Goldberg polyhedron system the number of: Vertices = 2(F – 2) and Edges = 3(F – 2) Where: F = the number of faces for the polyhedron sought.
The topological groups have been separated into three classes: Ref 10, 11, 12.
Class I “Subscript a is an integer and b is always zero or b is an integer and a is always zero. The lines of the triangular segmentation on the polyhedron face run parallel to the edges.”
Class II “Subscript b is an integer and is equal to a. The lines of the triangular segmentation on the polyhedron face run perpendicular to the edges.”
Class III “Subscript a and b can be any pair of integers as long as a ≠ b and a or b ≠ zero. The lines of the triangular segmentation on the polyhedron face run oblique to the edges.”
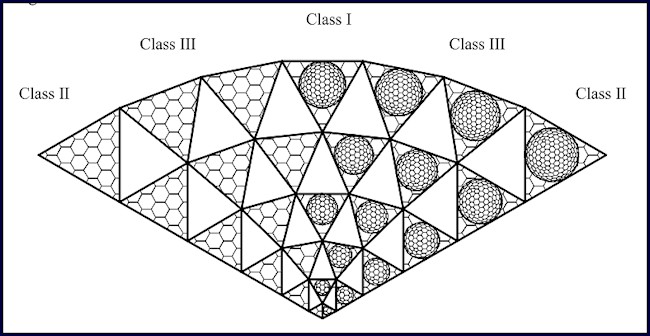
Figure 9. Goldberg polyhedra classes
THE CONJECTURE
A sphere may be tessellated in such a manner that it will be made up of a group of spherical polygons, with edges having equal central angles and having the topological characteristics of the Goldberg polyhedra.
THE GEOMETRY
A mathematical solution has not been found to prove the conjecture, however, enough Goldberg polyhedra having equal edge central angles have been found to convince this author that it has validity.
Twenty seven spherical tessellations of the Goldberg type have been found; nine each based on the icosahedron, octahedron and the tetrahedron. In each group 5 are of the Class I type, 3 are of the Class II type and, 1 the Class III type.
Tables 1 – 3 give their properties, and Figures 10 – 12 illustrate one face of the icosahedron, octahedron, or tetrahedron as a tessellated unit that would be repeated to develop the entire sphere. It should be pointed out that for the Class III types, an enantiomorphic of the one illustrated does exist for each one, but, are not shown here. One should also note that symmetry advantages of the Schwarz, Ref 13, triangle within each regular spherical triangular face can be used to an advantage when generating the forms. Each form in the figures will be identified by its base polyhedron, I, O, or T with a subscript a, b.
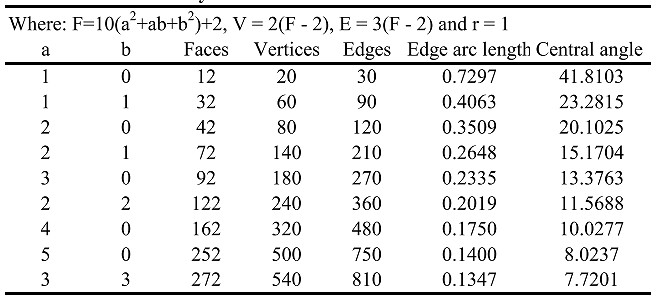
Table 1. Icosahedral System
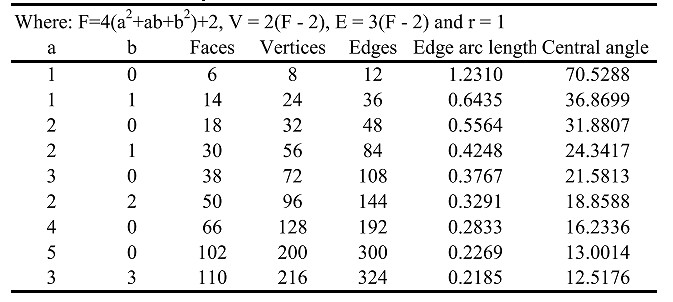
Table 2. Octahedral System
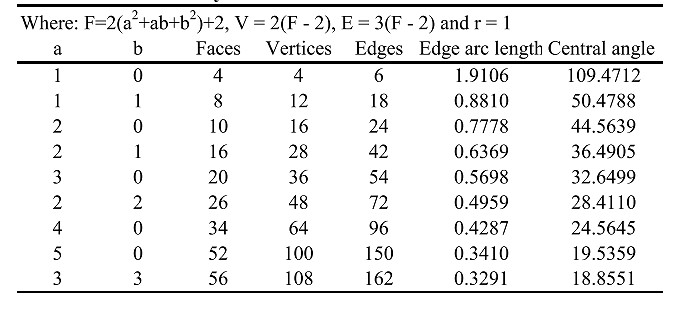
Table 3. Tetrahedral System
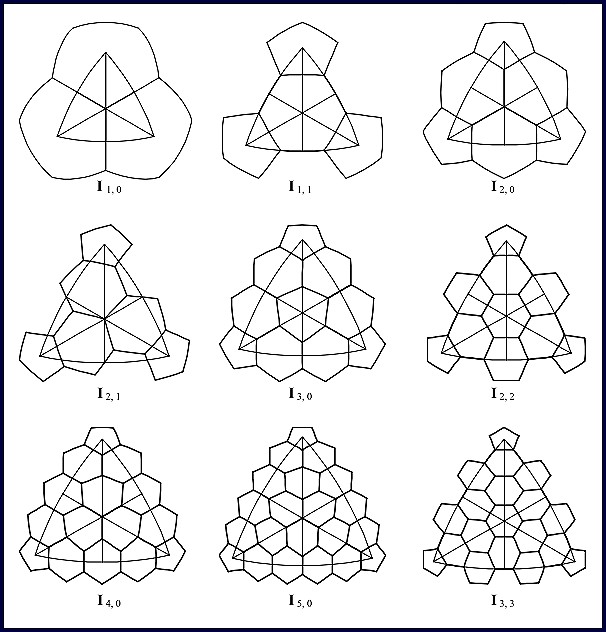
Figure 10. Icosahedral Goldberg equal central angle spherical tessellations
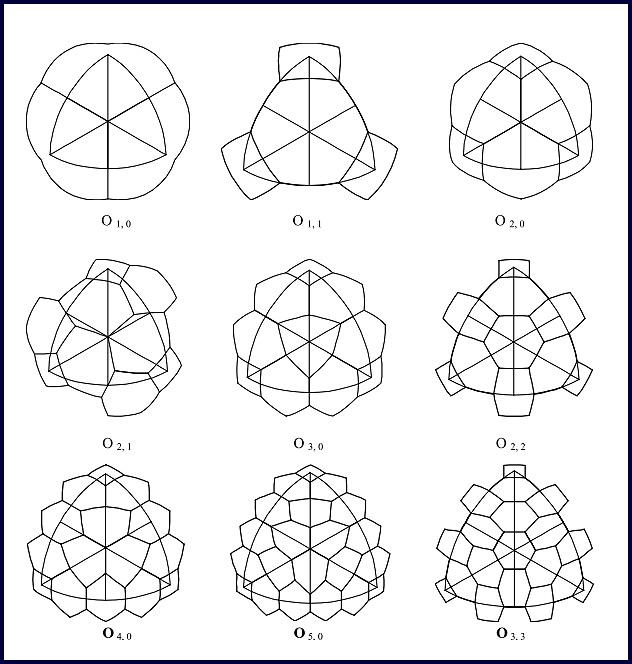
Figure 11, continued. Octahedral Goldberg equal central angle spherical tessellations
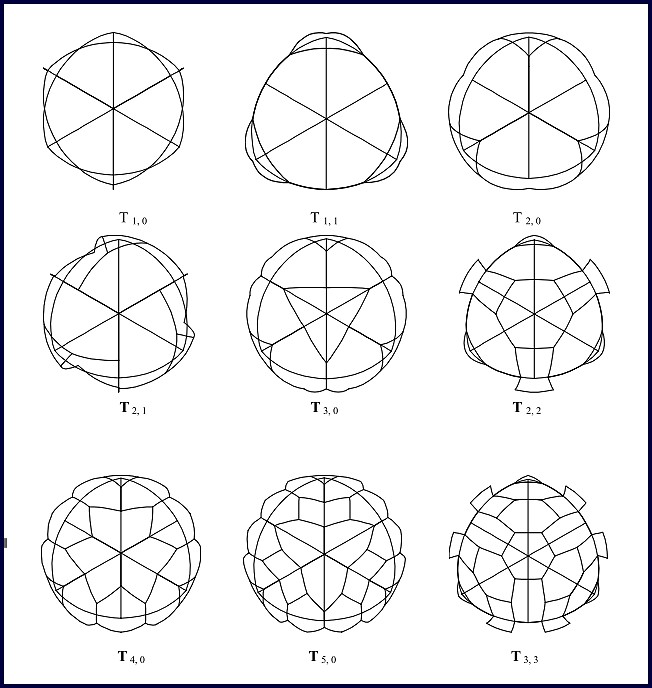
Figure 12. Tetrahedral Goldberg equal central angle spherical tessellations
ADDITIONAL RESEARCH
Hopefully one will find a mathematical solution to the problem of tessellating a sphere in such a manner that it will be made up of a group of spherical polygons, with edges having equal central angles and having the topological characteristics of the Goldberg polyhedra. In addition to this problem it may also be useful to study other spherical tessellated forms with edges having equal central angles. The diamond tessellations on the surface of a sphere appear to have similar characteristics. Ref 14 The Fullerenes described by Fowler Ref 15 using the spiral conjecture may also be a subject for investigation.
Since first proposing the conjecture stated herein in a paper to the 5th International Conference on Space Structures, held at the University of Surrey, Guildford, UK on 19-21 August 2002, it has come to my attention that Dick Fischbeck Ref 16 has been working on similar problem. He randomly arranges cones of consistent diameter on the surface of a sphere based on the spherical excess angle of a polyhedron. He has also proposed a variation where the central angles of the cones may consistently generate random tetrahedral pyramids that will tessellate the sphere. Perhaps a careful study of his RanDomes will provide a solution to the Goldberg polyhedra equal central angle problem
REFERENCES
1. GOLDBERG M, A Class of Mult-Symmetric Polyhedra, Tôhoku Mathematical Journal, vol 43, June 1937, pp 104-108.
2. FULLER B, Geodesic Structures, US Patent 3,197,927, August 3, 1965.
3. FULLER B, Inventions: The Patented Works of R. Buckminster Fuller, St Martin’s Press, New York, 1983, pp 214-226.
4. KROTO H W, HEATH J R, O’BRIEN S C, CURL, R F, SMALLEY, R E, C60: Buckminsterfullerene, Nature, vol 318, no 4, 1985, pp 162.
5. FOWLER P W, How Unusual is C60? Magic Numbers for Carbon Clusters, Chemical Physics Letters, vol 131, no 6, November 1986, pp 444-450.
6. SNYDER J P, An Equal-Area Map projection for Polyhedral Globes, Cartographica, vol 29, no 1, 1992, pp 10-21.
7. CARR D, KAHN R, SAHR K, OLSEN T, ISEA Discrete Global Grids, Statistical Computing & Statistical Graphics Newsletter, vol 8, no 2/3, 1997, pp 31-38. 8. SAHR K, WHITE D, Discrete Global Grid Systems, to appear in: Computing Science and Statistics, (1998).
9. Discrete Global Grid Research at Terra Cognita, http://bufo.geo.orst.edu/tc/firma/gg/


