Explaining strut length, vertex
Here is some basic information useful when calculating geodesic dome strut lengths and how to connect them together.
Struts lengths
All geodesic domes are made from joining struts of different lengths together. The more complex the dome, the more strut lengths you will have. The table below is for icosahedron-based geodesic domes (also referred to as “method 1″).
| Frequency | Number of strut lengths | Number of struts | Number of hubs | |
| 1V |  |
1 | 25 | 11 |
| 2V |  |
2 | 65 | 26 |
| 3V (3/8) |  |
3 | 120 | 46 |
| 3V (5/8) |  |
3 | 165 | 61 |
| 4V |  |
6 | 250 | 91 |
| 5V (3/8) |  |
9 | 350 | 126 |
| 5V (5/8) |  |
9 | 425 | 151 |
| 6V |  |
9 | 550 | 196 |
As shown above, the higher the frequency the greater number of struts are required and of varying lengths.
What is a vertex?

Simply put, the vertex is the end or tip of a strut. When you hear vertex to vertex, it means tip to tip. But technically it’s the meeting point of segments. When you see the word vertices it refers to a number of hubs. For example, in a geodesic dome made of conduit/pipe, vertex to vertex would mean hole center to hole center.
When you view assembly diagrams for timber or steel pipe geodesic domes, you’ll notice some struts overlap, some are screwed to be tip to tip, and others don’t even meet because they use hubs to hold the struts together.
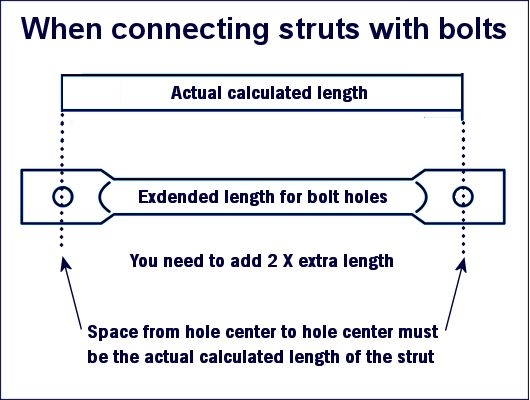
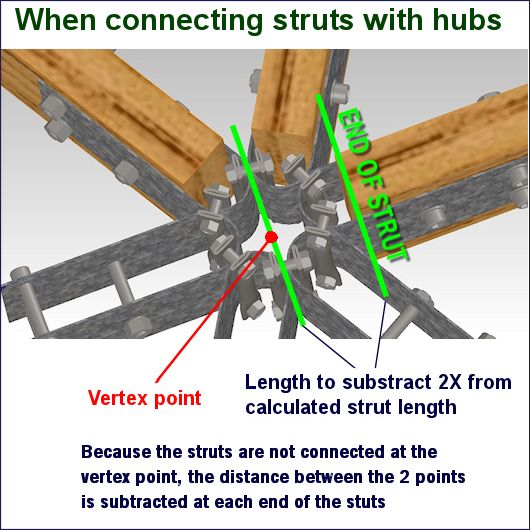
Whatever the method to connect the struts, the total length from vertex to vertex needs to be exactly what your calculations showed.
- If struts overlap (i.e. bolted together) you’ll need to make them longer to keep the correct length.
- If struts are connected with a hub, you need to subtract the length between the strut end and where they are supposed to meet. Subtract that length twice because both ends of your strut are connected to a hub.
- If you connect struts in a way that makes the strut end touch each other, then you have no addition or subtraction to make to your struts.
Look at the images below.