Geodesic Structure Analysis
The following is an actual structural report for a geodesic dome connector invented by Leith Aitchison of Domedimensions in Australia. Not only is this a very clever and sophisticated product, it was professionally analyzed by an engineering firm. Here below is the result.
For more information about Leith, his invention, diagrams and images, as well as Domedimensions, please click here.
For those who prefer to read the analysis in PDF format, here is the link to the document.
INTRODUCTION
The purpose of this report is to analyze the 9 meter geodesic dome manufactured by Dome Dimensions to determine the safe working load of the structure. It has been assessed in accordance with AS4100 for steel structures and AS1170 for loading conditions.

Figure 1: Dome Dimensions geodesic dome

Figure 2: Dome Dimensions geodesic hub joint
DOME CHARACTERISTICS
The geodesic characteristics of the Dome Dimensions 9 m dome are listed in Table 1.

Table 1: Dome Dimensions 9 m dome characteristics
The materials used in the construction of the Dome Dimensions 9 m dome are listed in Table 2.
The mass of the geodesic dome has been calculated using the items listed in Table 3.

Table 3: Dome mass
ASSUMPTIONS
The following assumptions have been made in this analysis.
- The canvas canopy has been represented as a series of vertical loads applied at each node. In reality there will be an additional horizontal component as the tarp tension acts in a direction normal to the dome surface.
- Wind loading is assumed to act in a direction parallel to the ground plane on the vertical projected area of the dome.
- It is assumed that working loads are suspended from the geometric centre of a node. In reality any mass suspended from a node will be attached via a bolt thus offsetting the load from the node centre. This will create a small torque component not accounted for in this analysis.
- The dome is assumed to be mounted on flat level ground
- It is assumed that each member on the base of the dome is fixed to the ground via a stake or similar means.
- The safe working load of this structure has been assessed against a serviceability state criterion and an ultimate state criterion. The serviceability state criterion is designed to ensure the structure does not experience any permanent deformation of parts under normal operating conditions. The ultimate state criterion is designed to ensure the structure does not collapse under the worst-case conditions, although some members may experience local yielding.
REFERENCED STANDARDS
AS 1170: 2002: Structural Design Actions
AS 4100: 1998: Steel Structures
AISC - ASD: Allowable Stress Design – Buckling of Compact Rolled Shapes
FAILURE MODES
This section examines the most likely cause of structural failure. The weakest member in the structure is determined by comparing the magnitude of the force for each failure mode.
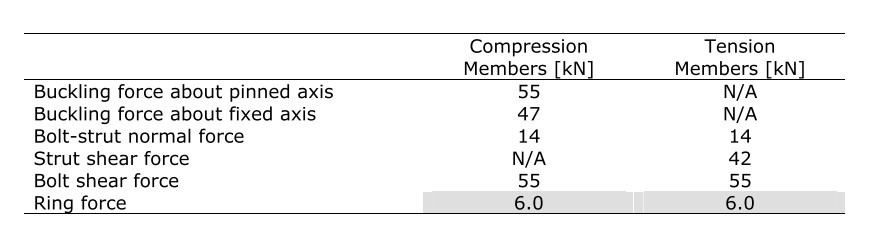
Table 4 lists each failure mode examined here with the corresponding strut force. It can be seen that the node is the weakest component in the structure and is expected to yield at approximately 6.0 kN of applied load from the strut.
Strut Buckling
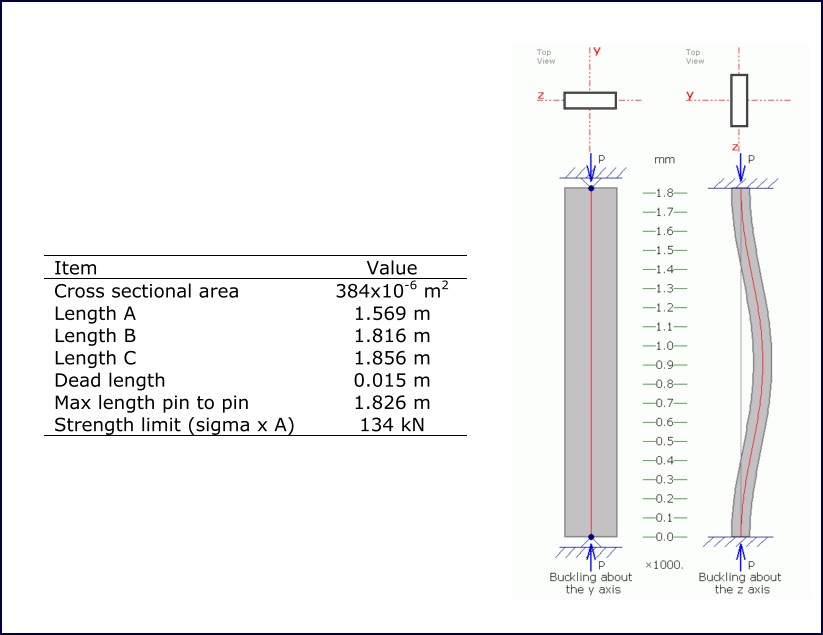
Table 5: Strut characteristics
Figure 3: Strut buckling analysis
The buckling strength of the longest member has been assessed in accordance with the AISC (American Institute of Steel Construction) standard using the allowable stress design (ASD) method for compact rolled shapes. The characteristics of each of the struts are shown in Table 5.
Table 6 shows the calculations used to determine the buckling strength of the longest member in both the pined and fixed axes. The strut is weakest in buckling about its fixed (Z) axis. Buckling is expected to occur at 47.2 kN.
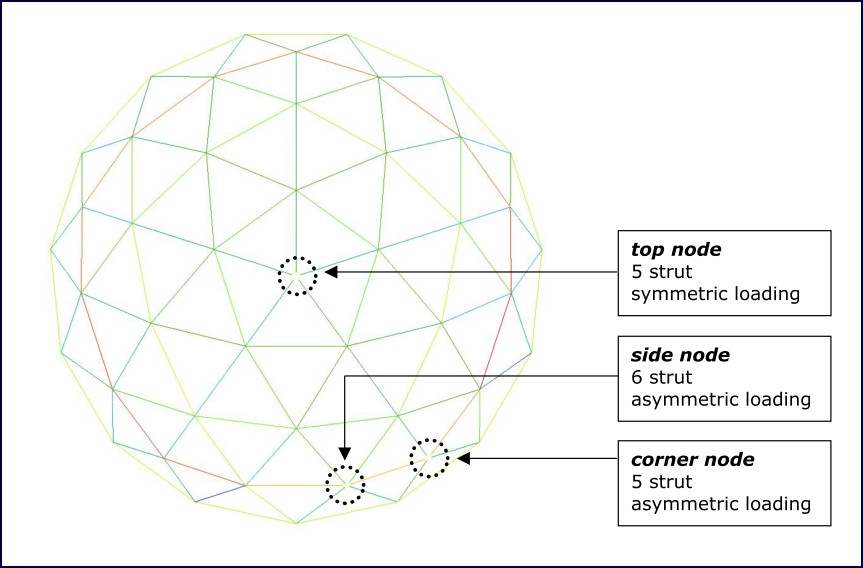
Table 6: Strut buckling calculations
Bolt Failure
Strut fasteners are M10, grade 8.8 button head cap screws. Table 7 shows the calculations used to determine the shear capacity of these bolts. These calculations have been completed in accordance with AS4100:1998. It can be seen that the nominal shear capacity of these bolts is 60 kN and the design capacity is 48 kN
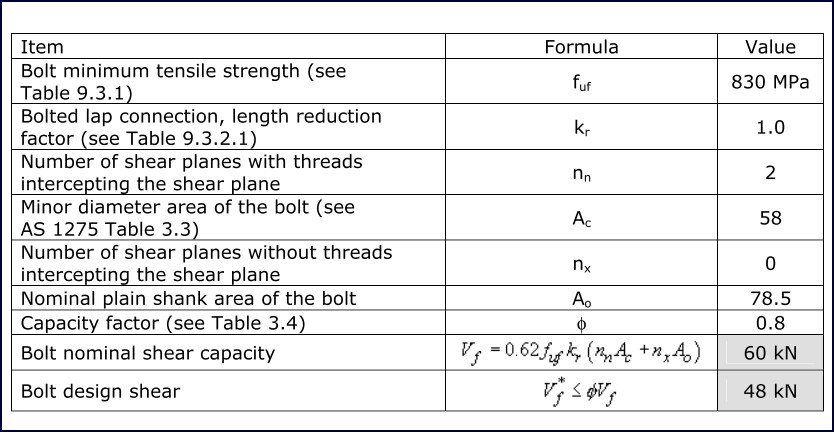
Table 7: Bolt shear capacity
The strut may fail in the region around the bolt due to localized stresses. Two failure modes have been investigated here. The strut may yield due to an excessive compressive force on the bolt-bearing surface; it may also fail in shear as the bolt tries to pull through the strut material holding it captive. The calculations in table 8 have been used to determine the approximate forces at which these failures will occur. It can be seen that the strut material will begin to yield in compression around the bolt at approximately 14 kN.
It should be noted that yielding in this region is not likely to result in a catastrophic failure of the entire structure it will simply cause an elongation of the bolt hole. This would only be a problem if this loading were experienced repetitively over an ongoing period of time.

Table 8: Local strut failure around the bolted connection
Node Ring Deformation
FEA analysis identified the ring to be the weakest component in the hub. The load carrying capacity of this ring was investigated using three methods, hand calculations, FEA analysis and experimentation. Table 4 below shows the results obtained from each method. It can be seen that no hand calculations or experimental data was available for the node with locking washers but it can be seen from the results of the analysis without locking rings that the FEA method was conservative. A nominal value of 6.0 kN was selected as the maximum allowable strut force. Figure 4: Node ring deformation estimates using various methods Strut Force [kN]
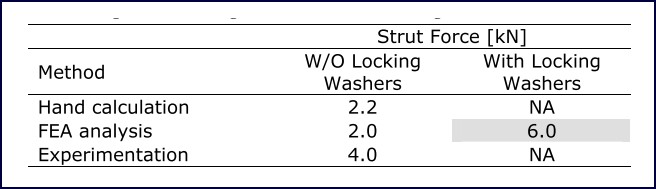
Figure 4: Node ring deformation estimates using various methods
Hand Calculations
Basic formulas for curved beams indicate the load carrying capacity of the ring is 2.2 kN applied at two points on opposing sides of the ring, as shown in the left hand example of Figure 5. The majority of nodes in the dome are subject to combined oads of compression and tension acting at right angles to each other as shown in the right hand example of Figure 5. The nominal force in each strut to cause deformation of the ring is therefore approximately 1.1 kN, or half that determined with curved beam theory.
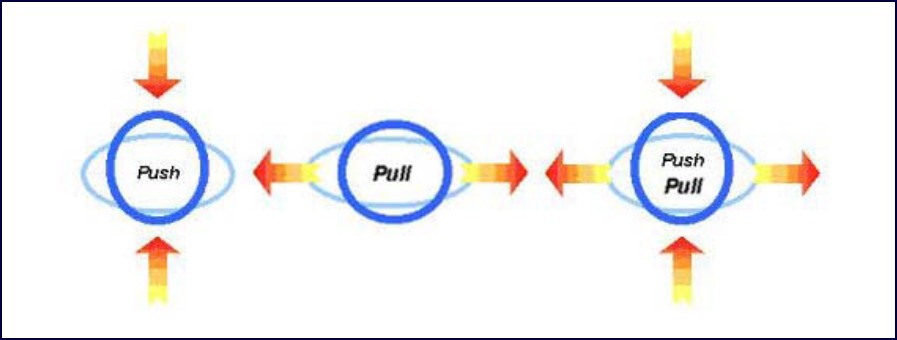
Figure 5: Combined effect of tension and compression on hub
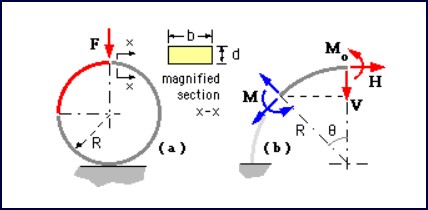

Table 9: Node ring calculations
FEA Analysis
To analyze the geodesic structure a 3D geodesic dome was modeled using simulated beams. Beam features simulated include material type, cross-section, orientation and end releases. Three nodes were modeled in the dome to assess what stresses were induced in the ring under various loading scenarios. The location of the three nodes is shown in Figure 6. The top center node was chosen because it is unique in that all attached members are in equally spaced and in compression. The two side nodes where chosen at the bottom of the structure because they carry the self weight of the structure, one of the nodes has five struts while the other has six.

Figure 6: Location of nodes analyzed on the structure
The dome model was loaded with masses at each node until the stress in the rings was in the vicinity of 210 to 240 MPa. The left hand column of Figure 7 shows a force of 2.0 kN in the struts was required to cause this level of stress. The addition of locking washers to the model raised the allowable force to between 6.0 and 12.0 kN depending on the node. This illustrates the importance of using the locking washers and also suggests that the ring will benefit from a permanent gusset welded to its centre. A nominal value of 6.0 kN was selected as the strut force maximum.
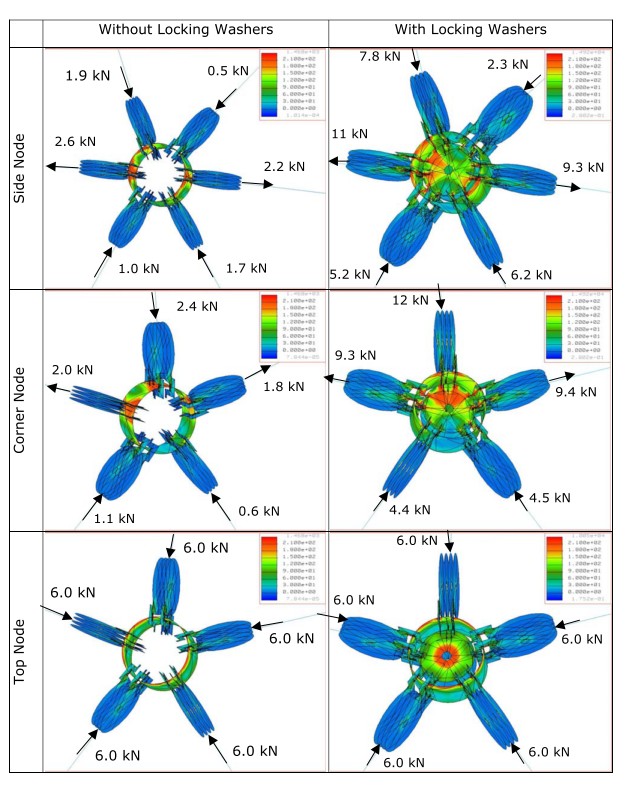
Figure 6: Location of nodes analyzed on the structure
Experimentation
A node ring was compressed between two flat surfaces to obtain a force deflection curve, the results can be seen in Figure 8. It can be seen that the ring yielded at 4.0 kN and its ultimate strength was in excess of 6.0 kN.
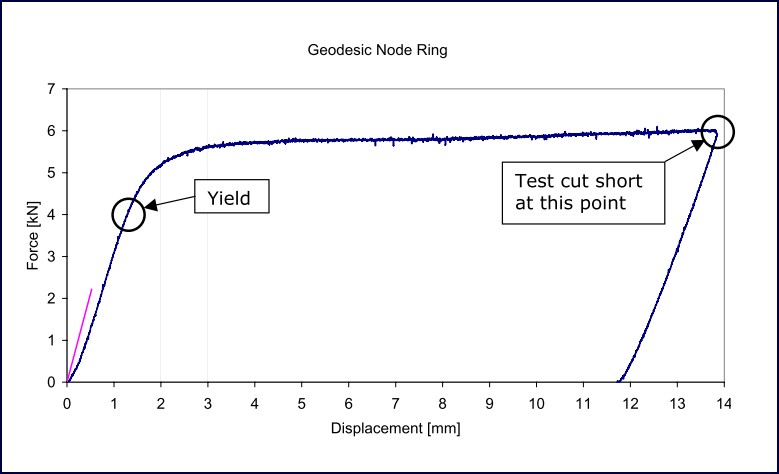
Figure 8: Node ring force – deflection curve
LOADS
This section determines the maximum allowable loads on the dome so as not to exceed the allowable strut for of 6.0 kN determined in the previous section. Loads investigated are wind loads and dead loads.
Wind Load
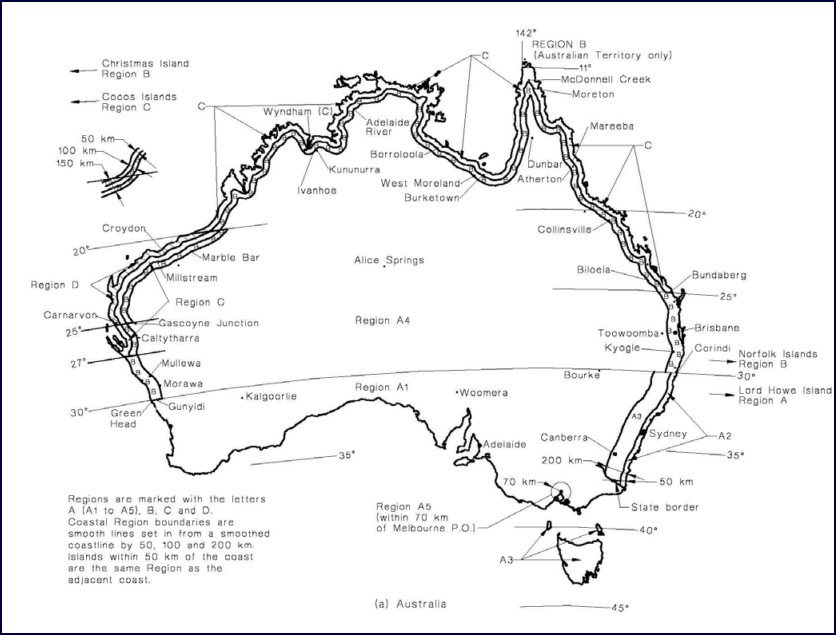
Figure 9: Wind speed regions
Figure 9 below shows the various wind regions throughout Australia. Region A was selected as the most appropriate for the dome. This means it can be erected anywhere in Australia, excluding cyclone affected coastal areas during cyclonic conditions (Regions B, C and D of AS1170.2: 2002).
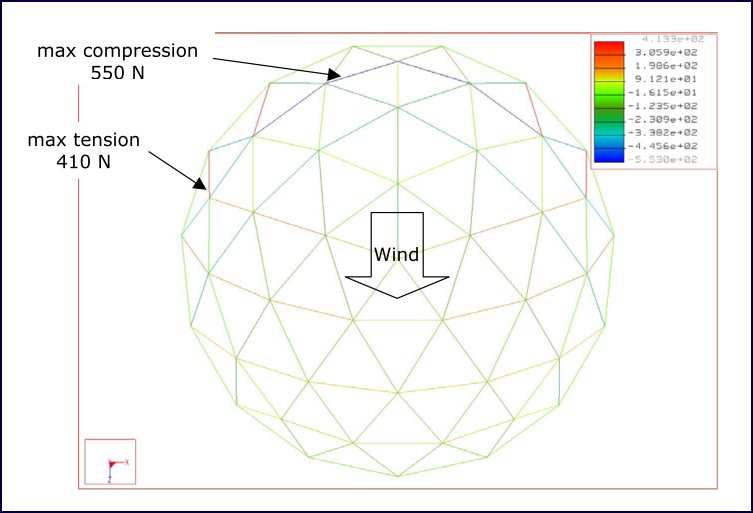
Table 10 shows the calculations used to determine wind loading in accordance with AS1170.2: 2002. It can be seen that for the serviceability limit state 550 N of compressive loading and 410 N of tensile loading must be allowed for. While for the ultimate limit state criteria 910 N of compressive loading and 680 N of tensile loading must be allowed for.
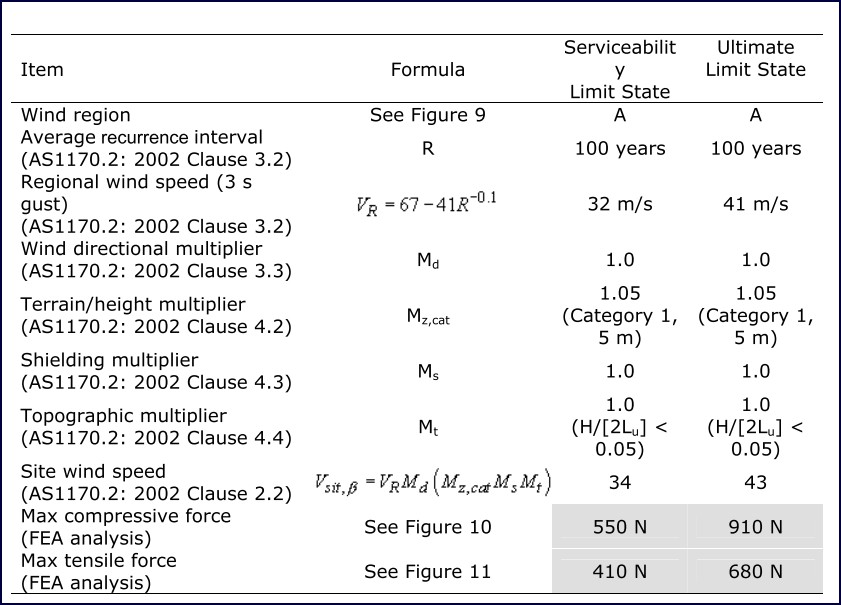
Table 10: Serviceability state site wind speed calculation
Figure 10 shows the forces induced in each member under the serviceability limit state criteria in region A wind conditions.
Figure 11 shows the forces induced in each member under the ultimate limit state criteria in region A wind conditions.
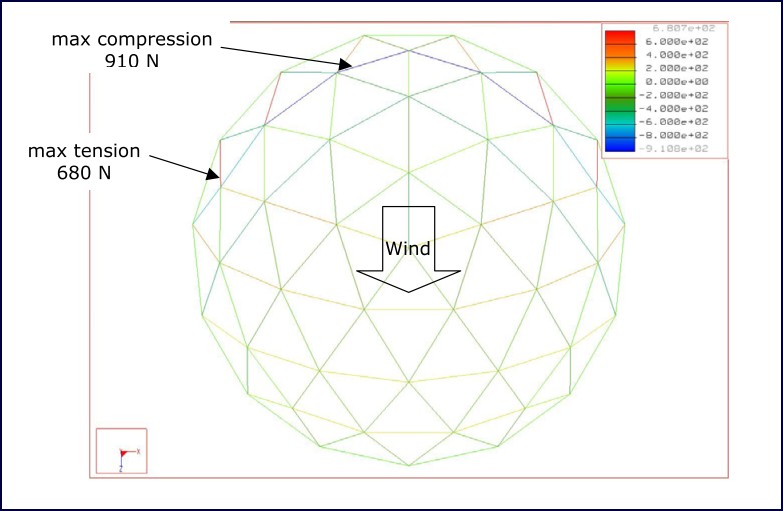
Figure 11: Beam forces under ultimate limit state
Dead Load
Figure 12 shows the forces induced in each member due to the structures own self weight.
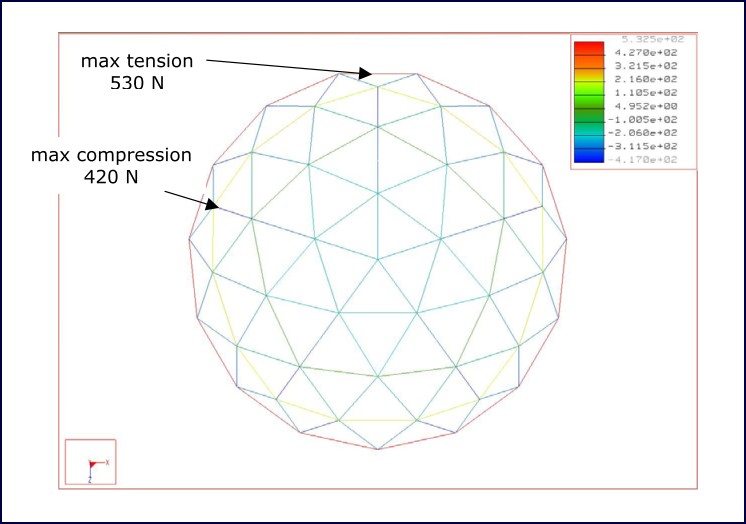
Figure 12: Beam forces due to structure dead weight
Combined Loading
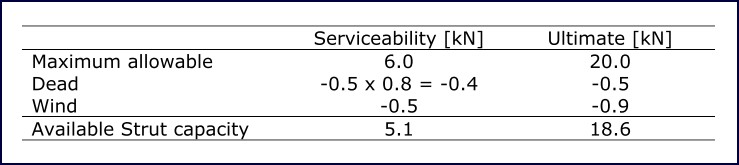
Table 11 shows the calculations used to determine the available strut capacity of the structure. It can be seen that the dome members have 5.1 kN of capacity to carry the safe working load.
Table 12 summarizes the safe working load of the structure so as not to exceed the capacity of the members determined in the previous section. It can be seen that 200 kg can be suspended from all nodes or 400 kg can be suspended from a single node.
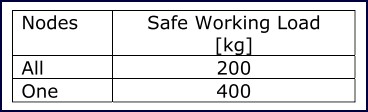
Table 12: Safe working loads
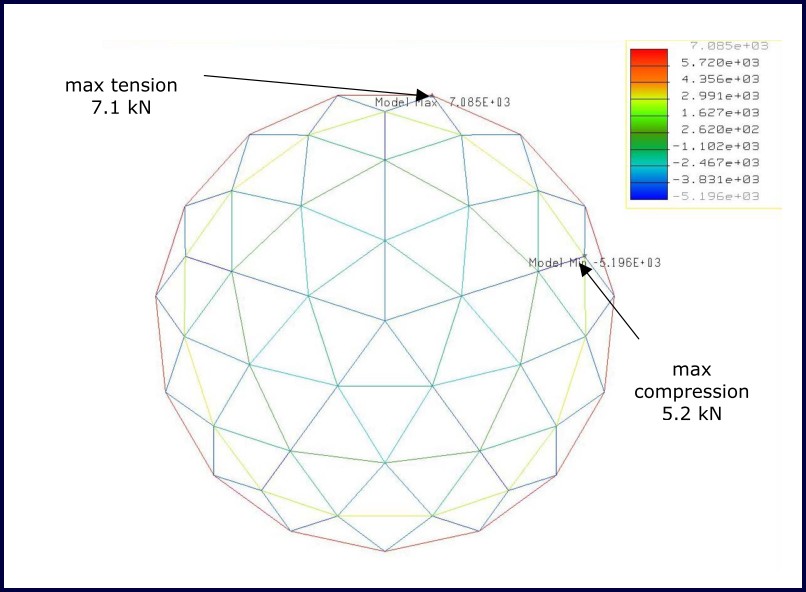
Figure 13 shows the maximum tension and compression force in the dome when 2000 N is suspended from each node. It can be seen that the allowable force of 5.1 kN is not exceeded.
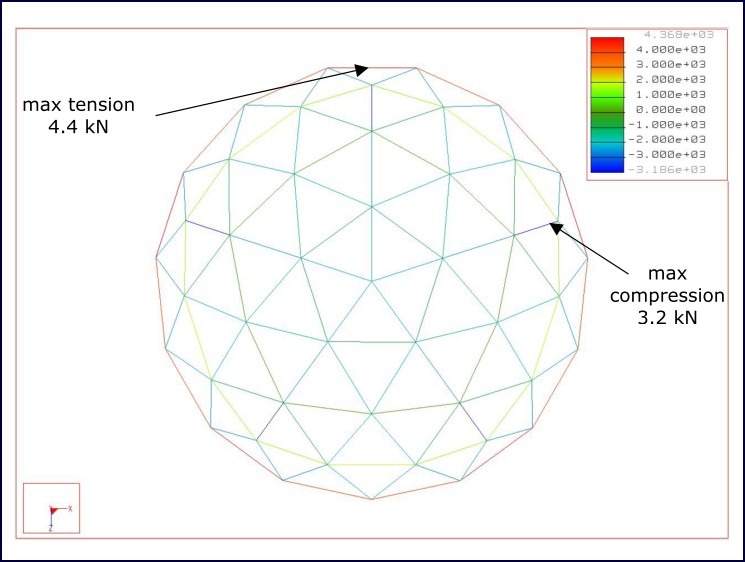
Figure 13: 2,000 N suspended from all nodes
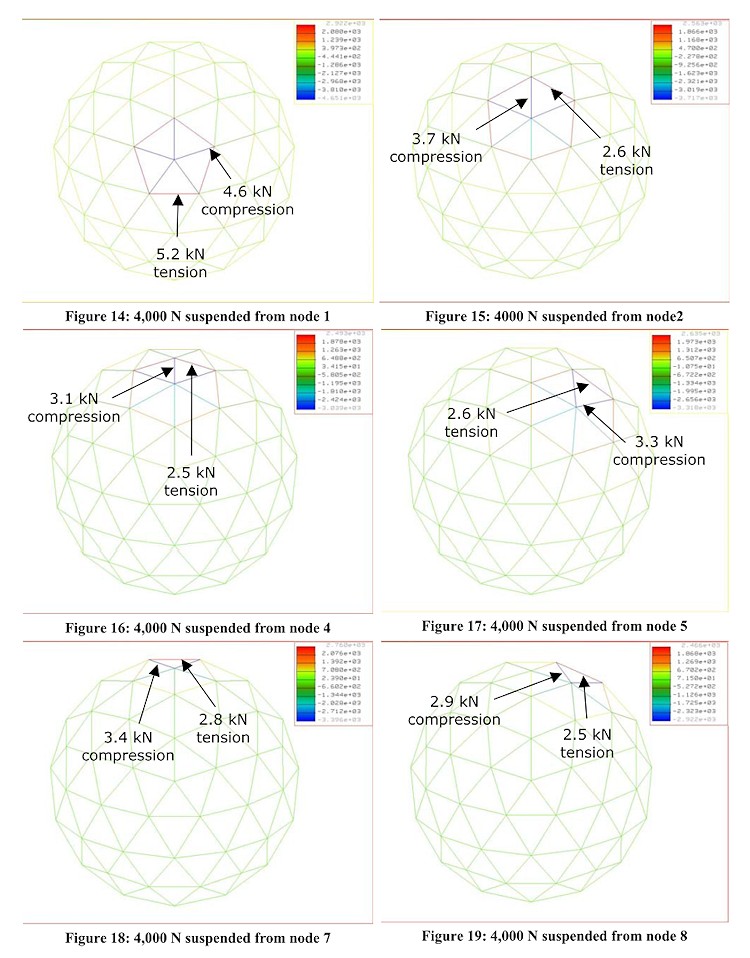
Figure 14 to Figure 19 shows the affect on the structure of suspending a mass of 400 kg from a single node. It can be seen that the allowable force of 5.1 kN is equaled in the case of node 1 and not exceeded in all other cases.
Overturning
To determine if overturning is likely to be a problem moments are taken about one edge of the dome. The overturning force is found to be 35.6 kN
Geodesic Analysis overturning
The wind velocity required to create a force of this magnitude is approximately 100 m/s which is well below the 30 to 40 m/s wind speeds used in region A wind calculations so overturning should not be a problem with this structure in region A winds.
MODIFIED NODE
The capacity of the dome increases substantially with the following changes, (see Figure 20).
- Gusset welded to center of ring
- Locking washes spaced further apart
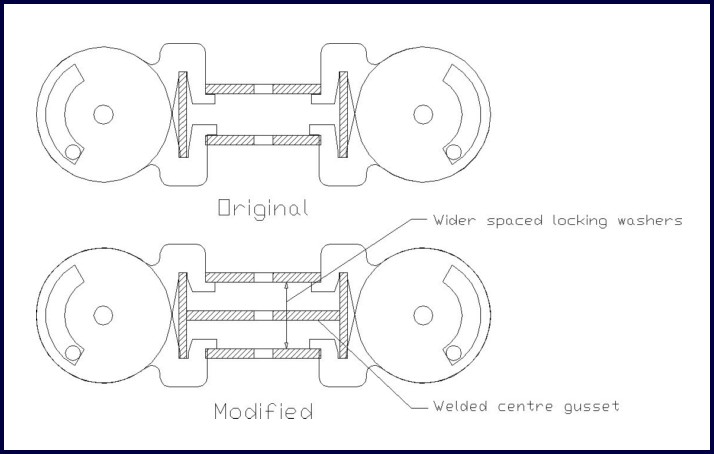
Figure 20: Differences between original and modified nodes
Finite Element Analysis
The modified node was compared to the original node using FE analysis. The results are shown in Figure 21. The modified node shows considerably less stress under a similar loading scenario raising the allowable strut force to around 9.0 kN.
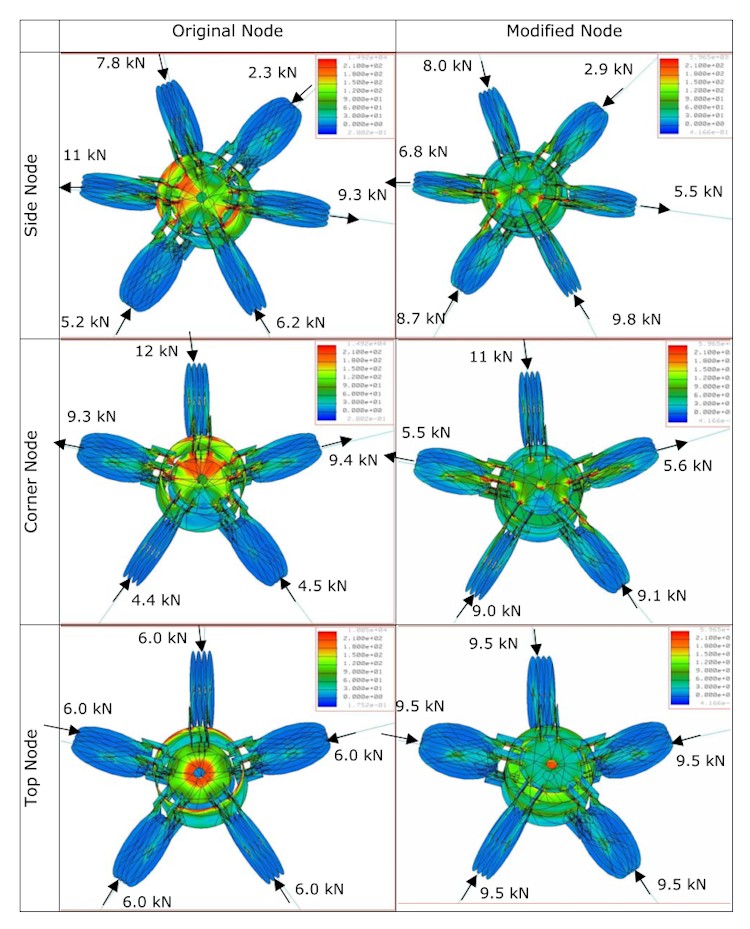
Figure 21: Comparison between strength of original and modifed nodes
Combined Loading
Table 13 shows the calculations used to determine the available strut capacity of the structure. It can be seen that the dome members have 8.1 kN of capacity to carry the safe working load.
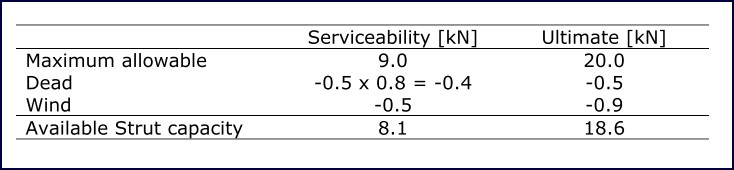
Table 13: Structure loads
Table 14 summarizes the safe working load of the structure so as not to exceed the capacity of the members determined in the previous section. It can be seen that 300 kg can be suspended from all nodes or 600 kg can be suspended from a single node.
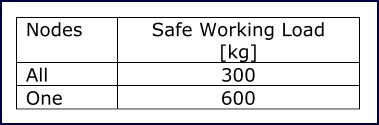
Table 14: Safe working loads for modified node
Figure 22 shows the maximum tension and compression force in the dome when 3,000 N is suspended from each node. It can be seen that the allowable force of 8.1 kN is not exceeded.
Taking the worst case single node loading found in the previous load cases Figure 23 shows the affect on the structure of suspending a mass of 600 kg from a single node. It can be seen that the allowable force of 8.1 kN is not exceeded in any of the members.
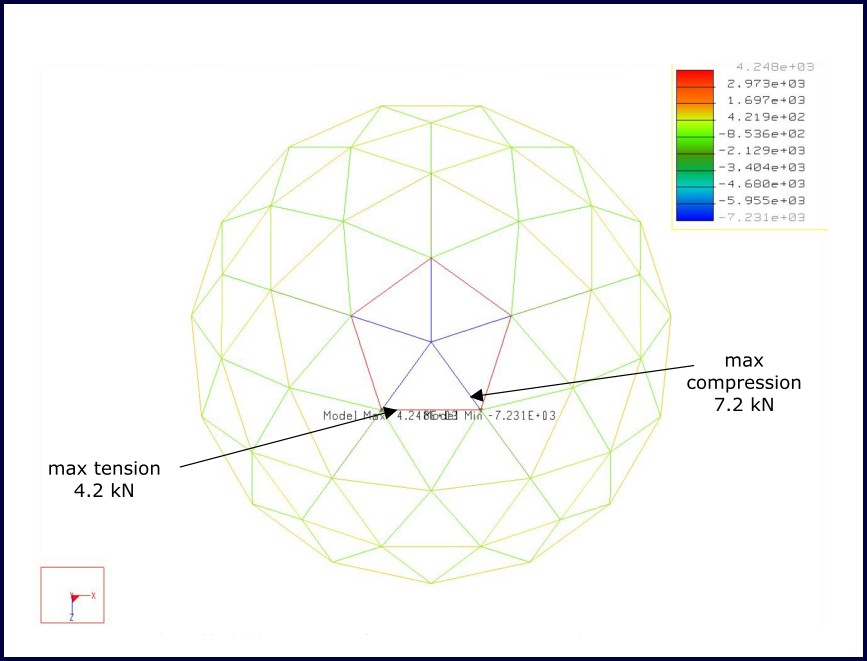
Figure 23: 6,000 N suspended from centre node (worst case single node loading)
SUSPENDED MASS FROM CENTER OF BEAM
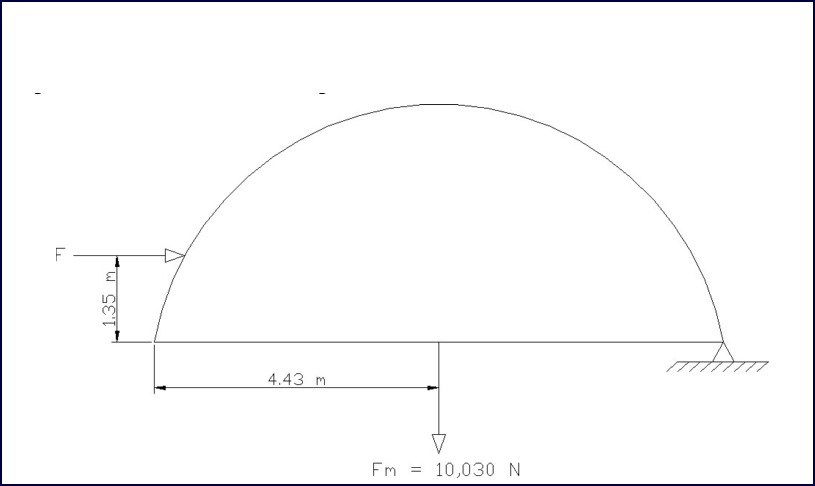
Horizontal members in the dome are typically in tension and therefore can carry a center hanging load without concerns of weakening these members due to buckling. The allowable load to be suspended from the center of a horizontal beam is given by:

The safe working load to be suspended from the centre of any horizontal beam is 30 kg. This assumes the beam is not weakened in any way by the method used to attach the mass. For example this does not allow for holes to be drilled into beam to attach fixing points.
CONCLUSION
The 9 meter Dome Dimensions dome has been analyzed in accordance with the relevant sections of AS 1170: 2002 (Structural Design Action), AS 4100: 1998 (Steel Structures) and AISC for buckling of compact rolled shapes. Two versions of the dome have been considered depending on the node type. One node is the original design with no center gusset and closely spaced locking washers; the other is the modified node with a welded center gusset and widely spaced locking washers. The safe working loads for the dome with the two types of nodes are listed below in Table 15.
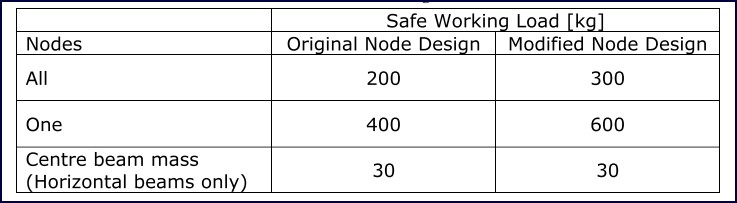
Table 15: Safe working loads
It is important to note that these safe working loads only apply when the locking washers used in the centre of the nodes are all in place as these are essential to the strength of the node. The structure is suitable for region A winds which means it can be erected anywhere in Australia, excluding cyclone affected coastal areas during cyclonic conditions (Regions B, C and D of AS1170.2: 2002).