Leveling the base of a dome
Most geodesic dome calculators on the Web don’t give a flat base — unless the structure is a a perfect hemisphere (a structure that when built results in using exactly half of a sphere, what you see most of the time), and that indicates the frequency (v) is an even number (2v, 4v, 6v, etc.). The geometry that’s typically used, so-called “method 1“.
The obvious question
So why not always build domes with the same geometric method and the same even frequency? Three factors: strength, simplicity and cost.
The most popular frequency is the 3v because it uses less struts which makes it easier, faster, and less expensive to build, but if you want a geodesic dome larger than 30 feet (12m) in diameter, traditional materials will not be strong enough. This means you have 2 options:
- Use better and stronger materials
- Increase the frequency of your geodesic dome
And this is how many people come to consider a different frequency.
Low profiles and high profiles
The calculator here, also known as a Kruschke method calculator takes a different approach, giving the dome a flat base for both the low-profile and high-profile versions (more or less than 1/2 of a sphere). The geometry was used by Buckminster Fuller in the early days of dome building. But the math wasn’t published until 1972, by David Kruschke, an American teacher.
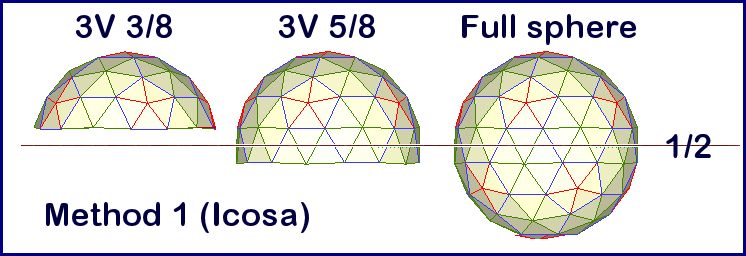
So when you see Kruschke, think flat or level base, whatever the “truncation” (where the dome is “cut”). For example, a typical dome is a 1/2 truncation because it is half of a sphere. Other truncations can be 4/9, 5/9, 3/8, 5/8 and so forth, but not all truncations are flat at the base.
Here’s an example: a 3v icosa geodesic sphere does not split into identical hemispheres. As we mentioned above, an odd frequency signifies that a dome will not be naturally flat at the base.
To make a dome, you can set the base either a little above the equator (center of the sphere), giving a low-profile “4/9” dome (4 rows of triangles), or a little below the equator, giving a high-profile “5/9” dome (5 rows of triangles). Many dome builders refer to 4/9 and 5/9 domes as “3/8” and “5/8” – terminology that dates back to the early days of geodesic dome design.
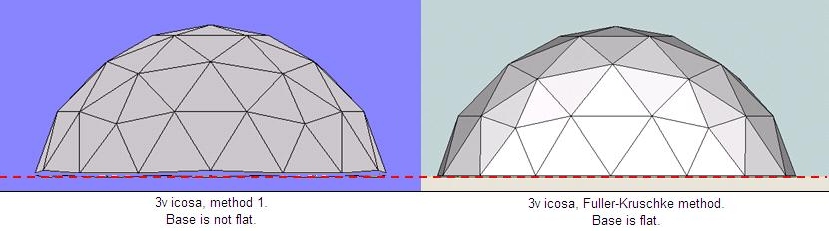
Unfortunately, method 1 geometry, the most used in building geodesic domes that you commonly see, gives an uneven base in both the low- and high-profile versions of the 3v dome. In other words, not all 15 nodes (where struts meet) lie in the same plane.
There are five ways to deal with this problem:
- You can shim the dome’s base, adding pieces of wood or other material to level the base
- You can shape the foundation to match the uneven up-and-down perimeter of the dome framework
- You can alter some of the strut lengths in the bottom row of triangles
- You can reduce the number of edges in the footprint from 15 to 10, which requires some clusters of triangles to be replaced by 5 trapezoids
- You can use an entirely different geometry whereby a flat base is built right into the dome design from the outset
Only the last option is a practical solution because it uses a different type of geometry to solve many issues.



