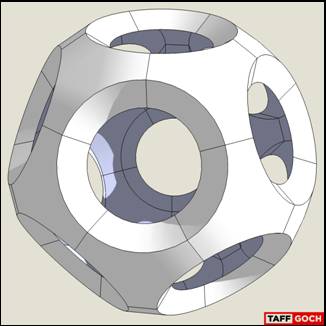
Spherical Dodecahedron
Uncle Dan (click on the banner below) has assembled the notes on a project that was initiated in the Google Geodesic Help Group. Below you can follow how participants came to offer instructions on how to build a spherical dodecahedron model made of paper.
You can download a Word document version of this page along with larger versions of the graphics by clicking here.
Taff: Dan might like this one. It’s simple; 20 identical parts. The folds are not straight lines, but arcs. I leave the connector tabs to you. If you want tabs added to the pattern, I can easily add them. You can, during assembly, cut off any superfluous tabs.
Dan: Taff,– This is definitely tempting. But first I am going to explore a little more origami.
Taff: Hmmm, — Are you sure I can’t entice you, with a full net….
Dan: Taff,– Oh, my goodness! It sure is pretty – need time to figure it out how it works. At the moment I am making a simple origami dodecahedron out of the very same gyroscope module I used to make the buckyball.
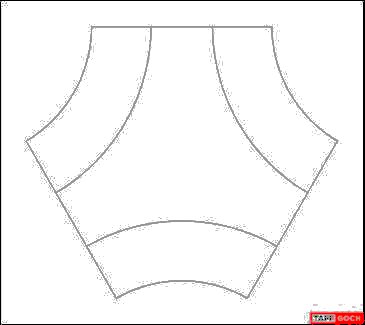
Taff: As a geometric note, the inner arcs ARE circular, but the outer arcs are NOT. When assembled, both, inner and outer arcs become circles, which are, indeed, planar. The outer arcs, in the net pattern, are not circular, because the “unfolding” of the edge of the spherical surface distorts the circle into an arc that approximates sections of 5 parabolas (parabolae?) It’s a minor deviation from a circular arc, and gave me fits, when trying to model it. At small scale, it probably wouldn’t be noticeable, either way.
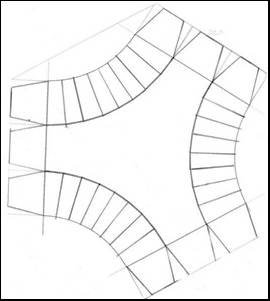
Dan: Well, I really didn’t understand how one could fold along a curve, so I suggested these modifications.
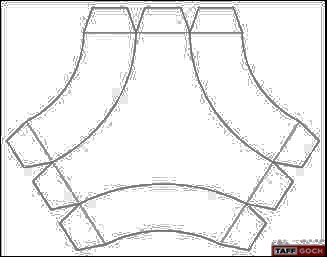
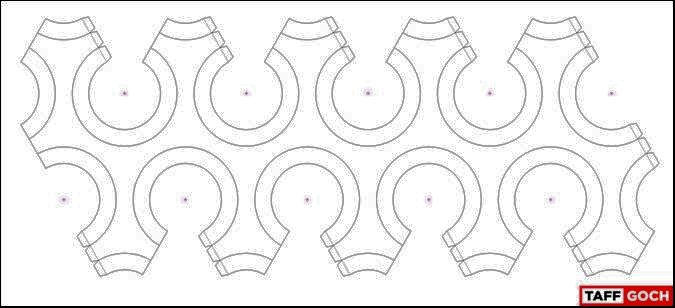
Taff: Dan, — Here’s the single-node pattern, with tabs. Obviously, you’re going to have to cut off some extraneous tabs, when assembling 20 together. I made the image large enough that you should be able to print a sheet-size pattern, without losing detail. Note that the only folds are curved folds. There are no straight folds to worry about. Let the paper take a curved shape, as you crease along the solid arc lines. It will take on the proper curved shape, on its own. (Pretty cool, actually.)
Dan: Taff, — It is surprising that it will allow itself to be folded along the curve. I may have to see it to believe it.
Taff: You have to “pinch” the paper, working along the line, a little pinch at a time. This style of folding has an online following, with some impressive examples….
Dan: Taff, — That was so easy. I never imagined this was even possible. It opens a whole new universe for me to explore. Thanks,–
Taff: Sorry, I fear that future exploration will keep you busy for life. The best search terms are:
Curved Folding: https://www.google.com/search?as_st=y&tbm=isch&as_q=curved+folding
Curved Crease: https://www.google.com/search?as_st=y&tbm=isch&as_q=curved+crease 568.2
Andrew: As a matter of trivia these structures are variations of Bucky’s fly eye dome. I always wondered how to make one, this is it.
Taff: Andrew, – First thing I thought, when I saw it. The paper model has the advantage of using a flat sheet of material. The curves are “simple” curves. (I.e,; they are not “compound” curves.) The fly-eye domes rely on the strength of compound curves, which is why the “curbs” extend outward, rather than in, as in the paper model. If a structural project is to be molded, then compound curves always provide much greater strength, and is the way to go.
Dan: Found this:
And also these pictures…..
__________________________________________________________________________________________
Dick Fischbeck: From our friend, Ron Resch. RIP. Video: https://vimeo.com/36122966
Taff: Thanks, Dick,– A worthwhile film to watch. It’s 41 minutes long, and I encourage readers to take the time to view.
Dan: Dick, — Thanks for posting the link to the Ron Resch video. I immediately watched the whole thing. Most interesting.
__________________________________________________________________________________________
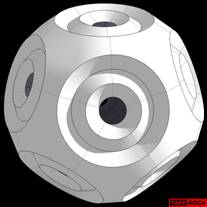
Dan: Taff, — Here are a couple of pictures of the completed model of the Spherical Dodecahedron.
That was fun. Thanks for talking me into it.
Taff: Great job, Dan, – Happy to have entertained your mind. I like your result so much that I’m going to make a physical model, myself, using sheets of flexible plastic from the local hobby store.
Dan: Taff, — Cool! Be sure to post pictures when it’s done.
You may have noticed that I used all the tabs and let them show. Made for a nice, strong connection.
Taff: Hey, Dan, how big is your finished model? It’s hard to tell, without any scale reference in your photos.
Dan: The diameter is about 14 inches. I just took your pattern, inserted into a Word Doc, with .5″ width border.
Taff: Nice size, for a shelf-display model….
You can download a Word document version of this page along with larger versions of the graphics by clicking here.
Learn about Uncle Dan’s OCTA-TETRA MUSEUM
See images of Uncle Dan’s OCTA-TETRA models by clicking on the logo:
