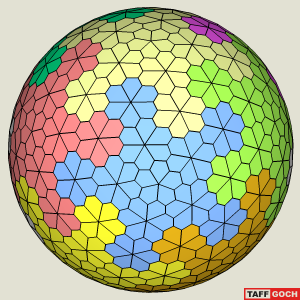
Floret Tessellation Sphere
During the summer of 2012, “Uncle Dan” took on the ambitious project of building a floret Tessellation sphere on his own. Daniel Suttin is a graduate of the Bronx High School of Science in New York City. He attended Renssalaer Polytechnic Institute in Troy, New York and then received his B.A. from the City College of New York. He continued at Boston State College completing courses which granted him certification in the state of Massachusetts as both an Elementary School teacher and as a teacher of High School Mathematics.
Since 2009 Dan has been employed half-time as a tutor at the “Developmental Math Lab” at San Antonio College. Students come into the lab and the tutors help with everything from Elementary Algebra all the way though Pre-Calculus.
FREE!
By email attachment, upon request to my email address, uncledan@homespun4homeschoolers.com , Uncle Dan’s “Algebra Workbook” file with matching “Solution Key” file, and any of my OCTA-TETRA files. For all 500 of them you can order the CD’s.
Learn about Uncle Dan’s OCTA-TETRA MUSEUM
See images of Uncle Dan’s OCTA-TETRA models by clicking on the logo:
Once upon a time, Uncle Dan…
When Taff, from the Google Geodescic Help Group, posted his Google SketchUp rendering of his “Floret Tessellation”, I decided I had to attempt a paper model.
 Class III 8,11 floret planar net |
 Class III 8,11 floret dodeca face symmetry |
Taff was kind enough to supply me with the templates. Click here to download them in .RAR format.
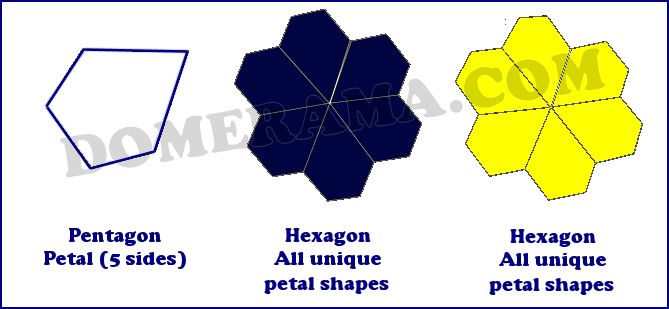
It was most interesting that the model was composed of 13 different “petals”. In the floret of each of the 12 pentagonal caps, each of its five petals was the same, but there were two other kinds of florets, both hexagonal, and the petals in each of those were unique.
Each hex Floret contains 6 different petals, for a total of 12 different petals. Each of the 12 petals is unique; no two are alike. The pent Floret contains 5 identical petals. So there are 13 different petals in all. So, all in all, there are 3 different Florets, one pent and two hexes.
So I printed out the pieces and did the cutting and scoring.
 |
 |
Then came the challenge of following the pattern to assemble the florets together. Several times, I found myself going “awry”, and had to backtrack a bit.
Along the way, it became apparent, that the model was chiral, and that since my florets were turned inside out, I needed to ask Taff to send me the “mirror” image of the completed sphere.
When I finally got the whole thing together, I found it too flimsy to resist the tendency to dimple and buckle under its on weight. I came up with a solution by running six dowels through the center of the thing from each pentagonal cap to its “antipode”. (Interesting fact, on the planet earth, less than 4% of land is antipodal to land.)
I contrived a way to hoist it up into the air, but one day, after about a month, it crashed to the ground. I managed to hang it again, but after a few days, it crashed again. At that point, I didn’t have the patience to fiddle with it any more, and so I trashed it. But at least I have the pictures of the entire project. It was the process that mattered, more than the finished product.
