More Models
So far, I have dealt with forms generated from the icosahedron and a subdivision parallel to the original icosa face sides.
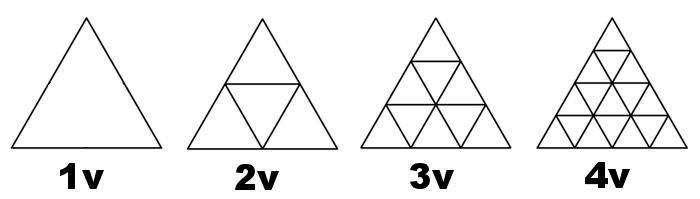
This can be called the “Alternate Breakdown”. This image below from part 1 describes this breakdown resulting in higher frequencies everytime you subdivide.
There is another type of breakdown, and for this we must go back to the original icosa triangle. Instead of drawing lines parallel to the triangle’s sides, we draw lines peggendicular to them.
This is called the “Triacon Breakdown.”
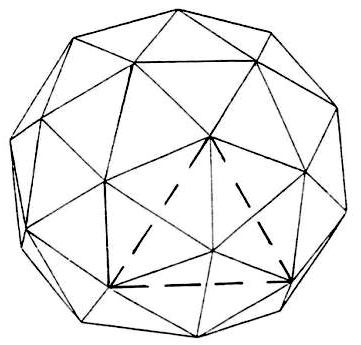
2v Triacon
Icosa face shown dotted

4v Triacon
Icosa face shown dotted
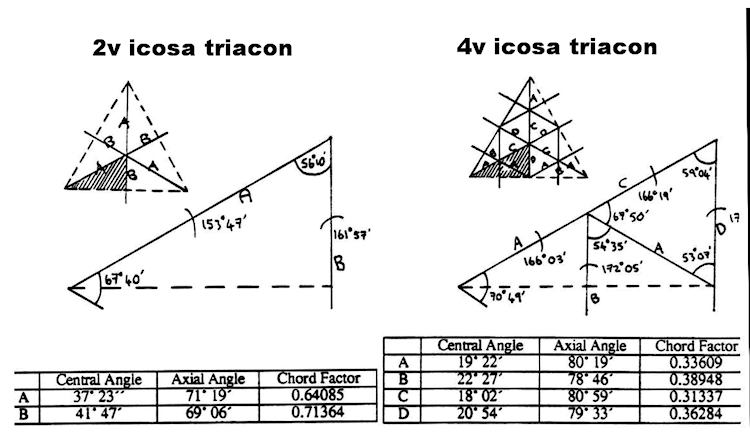
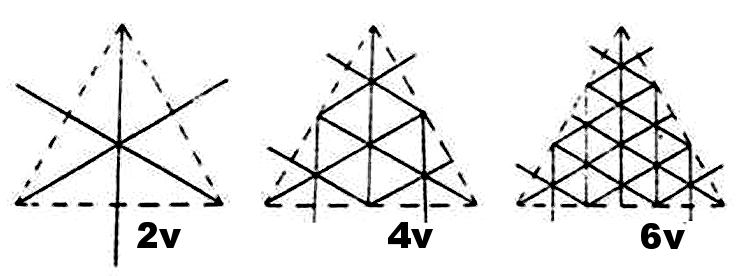
There are some interesting differences between the Alternate and Triacon breakdowns. Since the triacon breakdown is symmetrical about a line drawn down the centre of the icosa triangle, the triacon is only possible in even frequencies. The alternate, however, is possible in all frequencies. In even frequency alternate breakdowns (2v, 4v, 6v) great circles are formed which divide the sphere neatly into hemispheres.
The triacon breakdown does not have this feature in any frequency. ln order to make a triacon half-sphere. some triangles have to be cut in half. The triacon requires fewer different lengths because of its higher symmetry, but. on the other hand. the struts vary in length more than in the altemate breakdown.
Try a model and see the differences.
To make a 4v triacon sphere you will need:
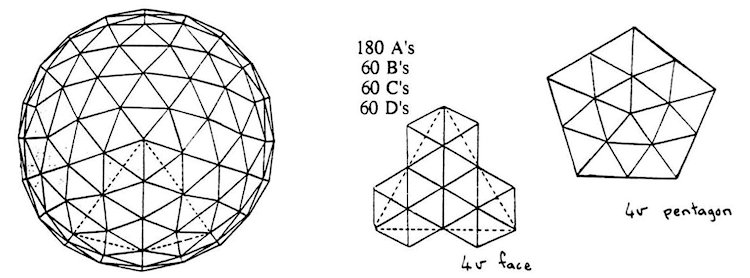
By now you should ?nd it fairly easy to identify different types of domes. What you do is look for a point where ?ve struts join. Then ?nd another pentagon and draw a line between them. If this line is de?ned by actual struts. then the dome is an altemate breakdown. If there are no stmts along the line. the dome is a triacon. What you are doing is picking out comers of the original icosa. The line you draw between them is an icosa edge. and counting the number of parts into which it is divided gives you the frequency of the dome.

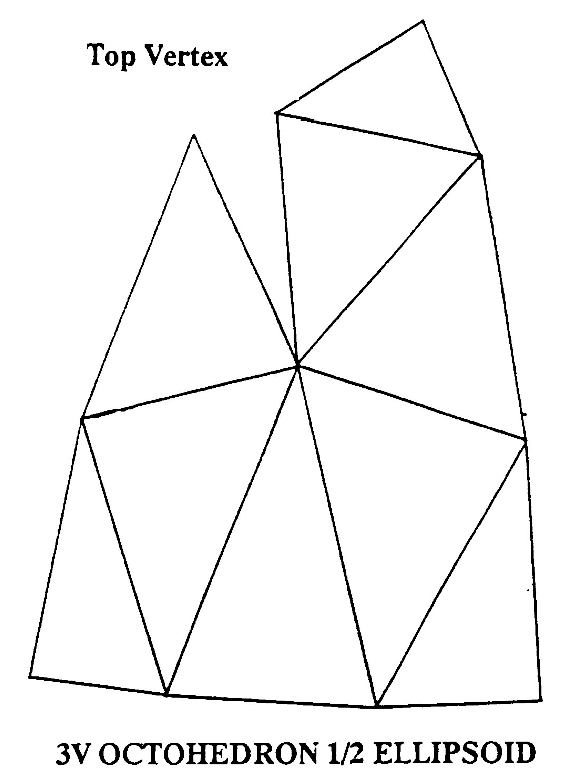
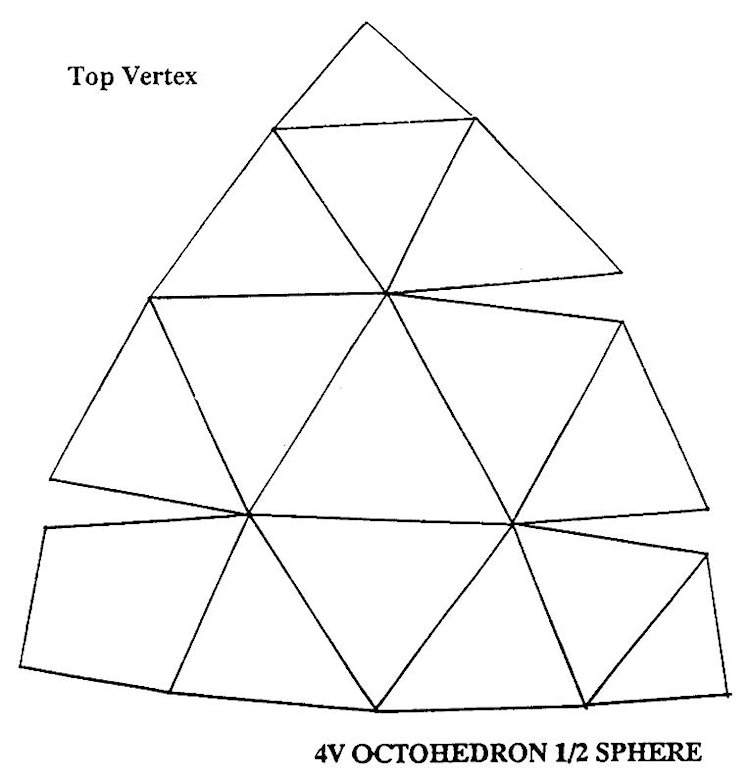
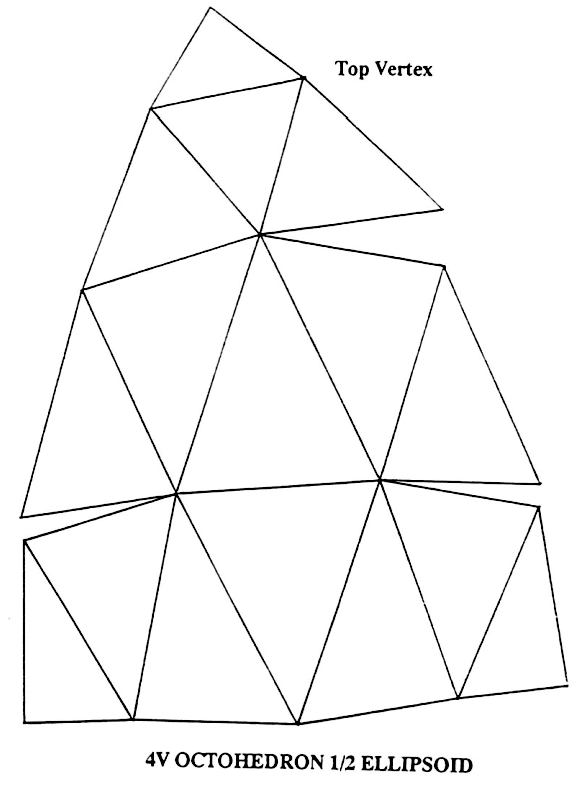
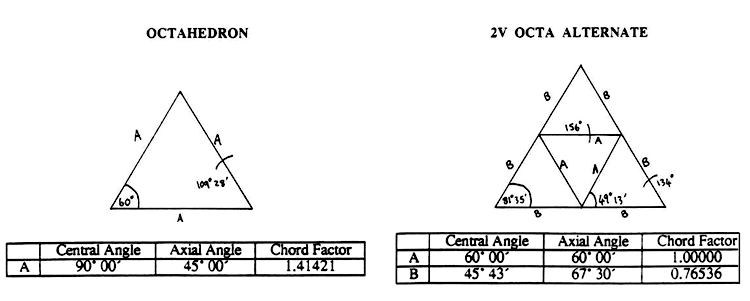
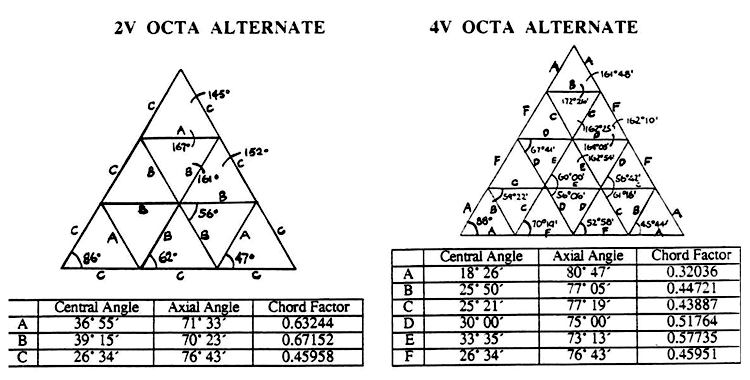
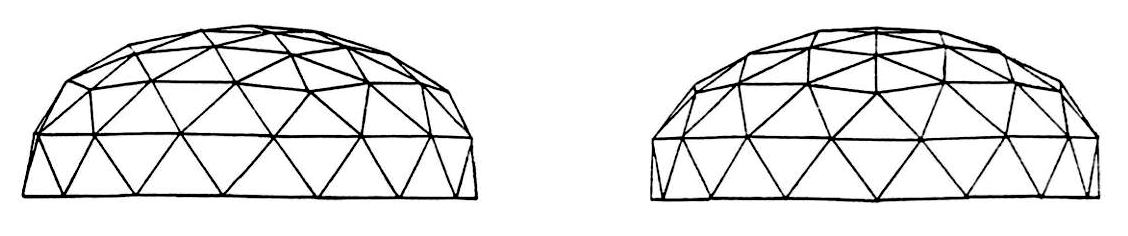
Domes can also be generated from the Octahedron. They are not as round as domes generated from the icosahedron and can be easily recognised by a square where the eight octa faces meet. The Octahedron form has the distinguishing ability to be able to fuse to rectilinear forms. The Octahedron also forms a natural truncation at the hemisphere.
Assembly methods are as follows:
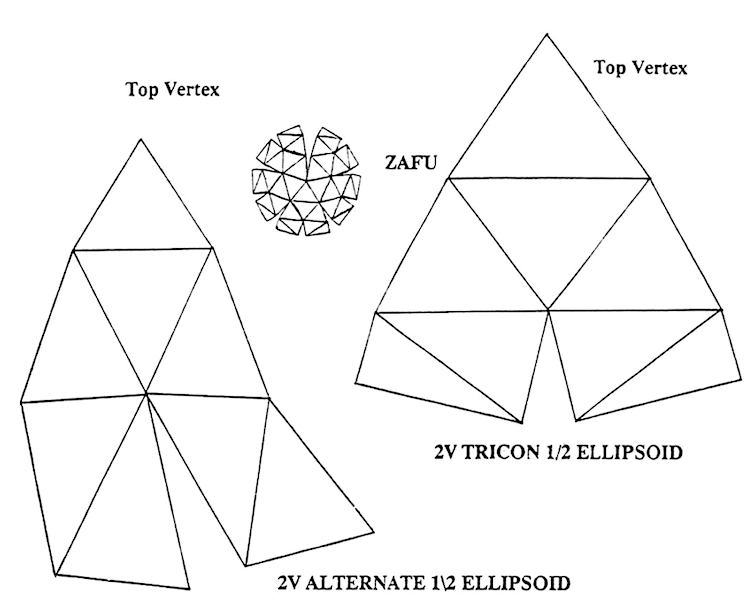
Domes can also be squashed or stretched to give an ellipsoidal form.
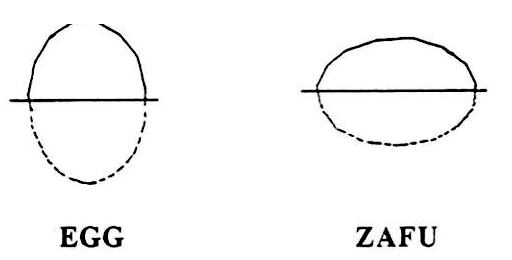
These forms are useful if building big domes where the dome is squashed down to save both headroom and surface area.
THREE FREQUENCY ICOSAHEDRON ELLIPSOID (SQUASHED)
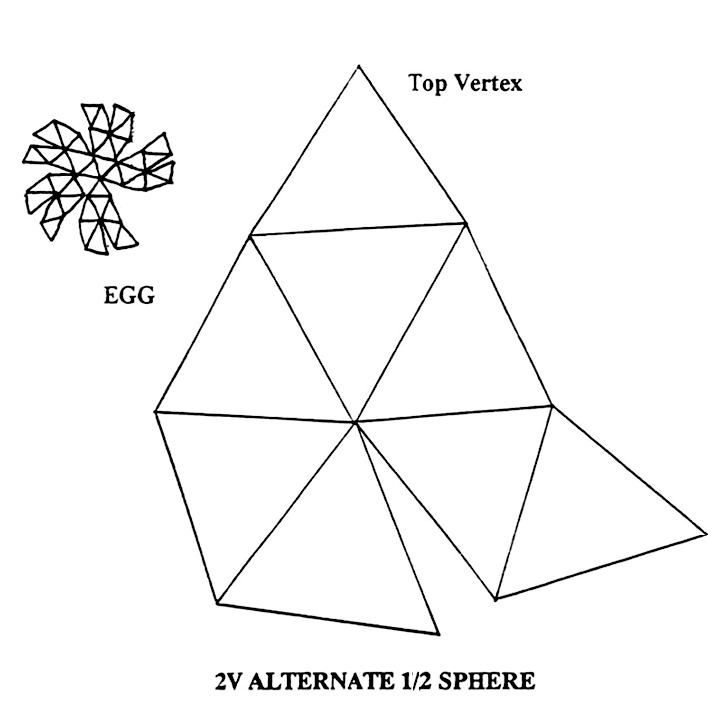
One last word on model making is to make paper or cardboard models. Use the patterns on the following pages. Punch with a pin through the paper onto thin cardboard. or trace onto paper.
Trace ?ve times for the Icosahedron based domes, four times for the Octahedron based domes. Either tape the gathering angles to form curved sections or add tabs on the edges which can be glued or stapled together inside. Very attractive scale models can be made by using artist’s mount board and gluing the edges together on the insides with a hot glue gun.
In calculating dimensions. the following formulas are useful:
π = 114159265
CIRCUMFERENCE OF A CIRCLE = 2 * π *R
AREA or A CIRCLE = π * R²
AREA or A SPHERE =4 * π * R²
VOLUME OF A SPHERE = 4/3 * π * R³
AREA OF A TRIANGLE = 1/2 * BH
4v ICOSA ALTERNATE
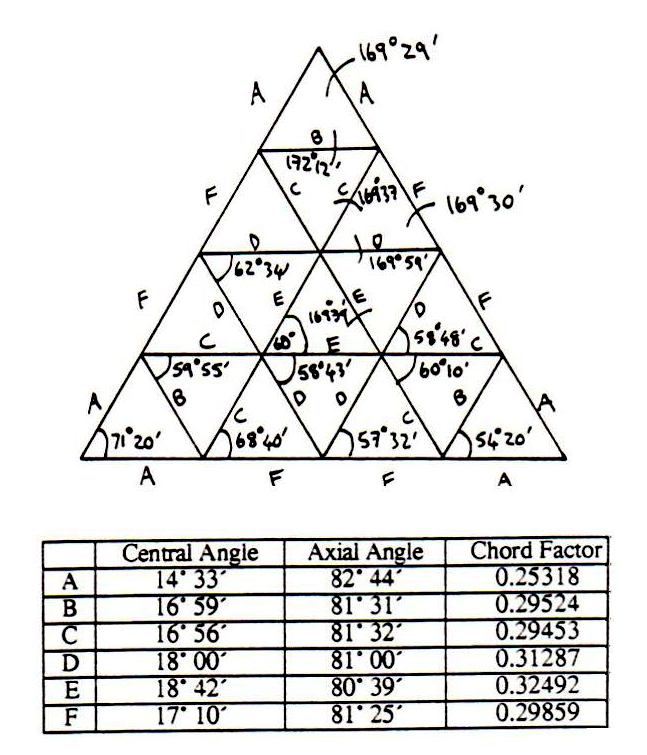
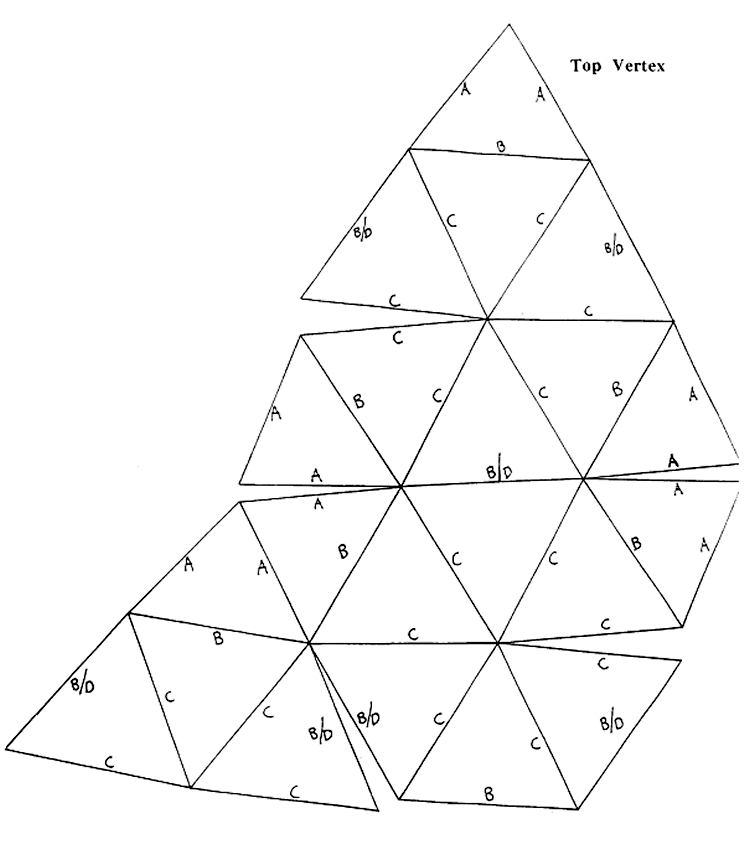
3v ICOSA ALTERNATE 5/8 SPHERE (MAKE 5)